图的存储结构以及深度优先遍历-C语言版
温馨提示：
本文最后更新于 2021年09月04日，已超过 1,204 天没有更新。若文章内的图片失效（无法正常加载），请留言反馈或直接联系我。
前言
学完图的深度优先遍历算法后，如何将我们的逻辑思维通过代码来实现呢？由于书中给的都是伪代码，所以这里大家实现了一下。
一、图在计算机中如何存储呢？
图跟其他数据结构类似也有两种存储结构那么就是，顺序存储结构和链式存储结构。
1.顺序存储
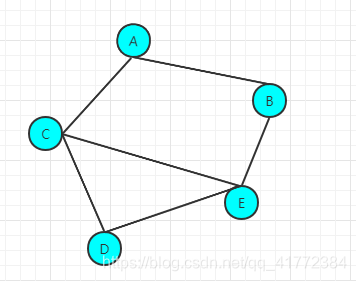
那么，现在有一个如下的图，需要采用顺序存储结构来存储到计算机中。是如何实现的呢？
我们通过一维数组来存储图的顶点，通过邻接矩阵（二维数组）来存储边。 这样我们就可以通过计算机来描述这个图了。
邻接矩阵：表示顶点间相邻关系的矩阵
一维数组
通过一个一维数组来讲图中的ABCDE五个顶点依次存储到图中即可，如下图：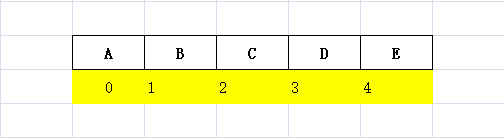
当然有时候我们顶点不仅仅只代表一个字母，或许还有更多的含义，那么我们就可以通过定义一个顶点结构体来描述顶点的信息。
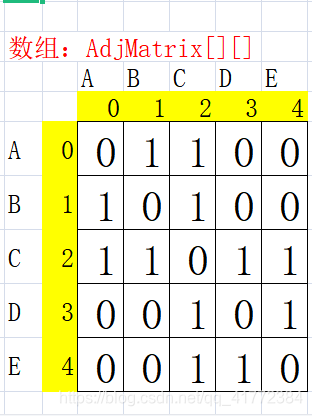
二维数组（邻接矩阵）
图中二维数组AdjMatrix[0][1]=1 代表顶点AB之间存在边，AdjMatrix[2][0]=1 代表顶点CA之间也存在边。
代码实现顺序存储结构
#include<stdio.h>
#define MAX_VERTEX_NUM 20 //最大顶点数
/*
*采用邻接表存储无向图
*无论哪种存储结构，都需要想办法来构造结构存储 顶点集和边集
*/
typedef struct{
char vexs[MAX_VERTEX_NUM]; //一维数组存储顶点集
//int vexs[] = {1,2,3,4,5}; //根据顶点的类型来选择存储顶点的数组类型，复杂的顶点可以定义结构体来存储
int AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //邻接表存储边集
int vexnum,arcnum; //图中顶点数和弧的数量
} MGraph;
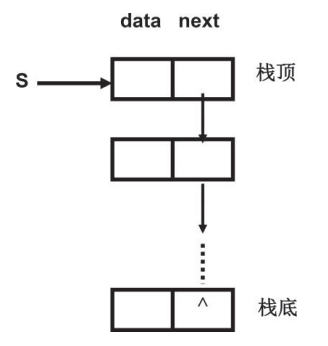
2.链式存储结构
见下一篇博客
二、将图存入计算机中
由图中我们可以看到一共有五个顶点（A、B、C、D、E）和六条边（AB 、AC 、CD 、CE 、DE 、BE ）。
1.存入顶点
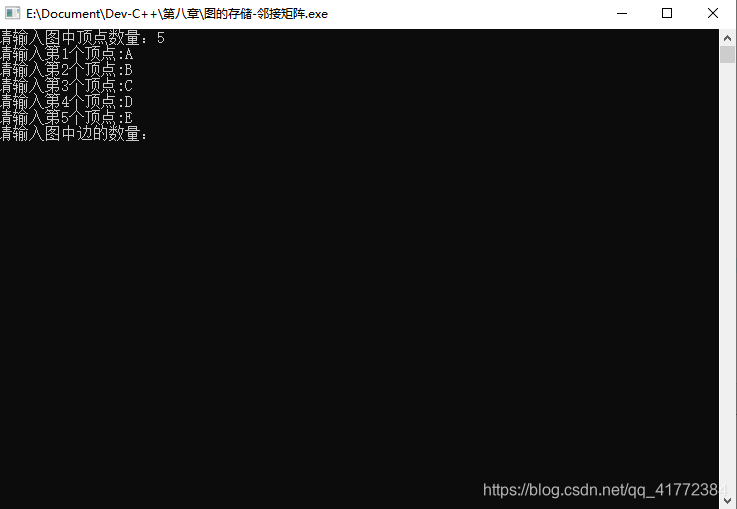
2.存入边
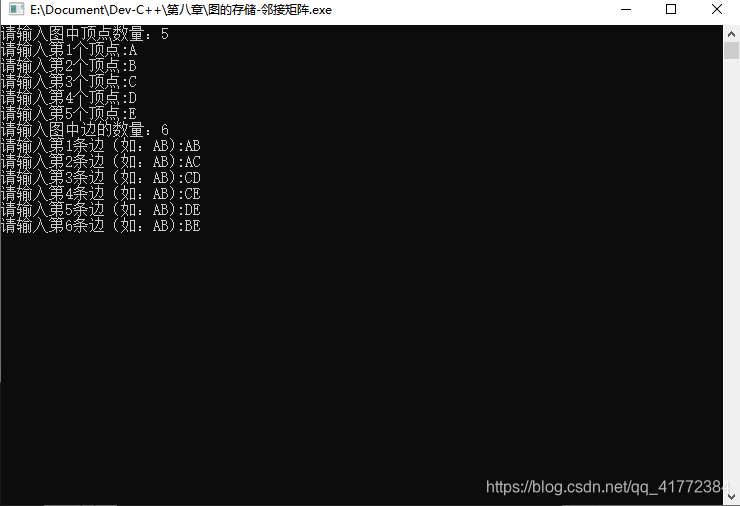
三、深度优先遍历
我们以A顶点开始遍历那么遍历的一个结果为：【ABECD】
深度优先遍历代码实现
#include<stdio.h>
#define MAX_VERTEX_NUM 20 //最大顶点数
/*
*采用邻接表存储无向图
*无论哪种存储结构，都需要想办法来构造结构存储 顶点集和边集
*/
typedef struct{
char vexs[MAX_VERTEX_NUM]; //一维数组存储顶点集
//int vexs[] = {1,2,3,4,5}; //根据顶点的类型来选择存储顶点的数组类型，复杂的顶点可以定义结构体来存储
int AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //邻接表存储边集
int vexnum,arcnum; //图中顶点数和弧的数量
} MGraph;
/*定位顶点在图中的位置*/
int LocateVex(MGraph G,char vex){
for(int i=0;i<G.vexnum;i++){
if(G.vexs[i] == vex)
return i;
}
return -1;
}
/*创建图*/
void CreateGraph(MGraph &G) {
/*初始化图的基本信息*/
//输入图中顶点
printf("请输入图中顶点数量：");
scanf("%d",&G.vexnum);
for(int i=0;i<G.vexnum;i++){
printf("请输入第%d个顶点:",i+1);
scanf(" %c",&G.vexs[i]);
}
//输入图中的边
printf("请输入图中边的数量：");
scanf("%d",&G.arcnum);
//初始化邻接矩阵
for(int i=0;i<G.vexnum;i++){
for(int j=0;j<G.vexnum;j++){
G.AdjMatrix[i][j] = 0; //初始化时顶点间都不存在边
}
}
//构造邻接矩阵
for(int k=0;k<G.arcnum;k++) {
char v1,v2;
printf("请输入第%d条边（如：AB):",k+1);
scanf(" %c%c",&v1,&v2);
int i = LocateVex(G,v1); //获取边第一个顶点在图中的位置
int j = LocateVex(G,v2); //获取边第二个顶点在图中的位置
G.AdjMatrix[i][j] = 1; //存在边就设置为1
G.AdjMatrix[j][i] = 1; //由于是无向图所以相反反向也存在边
}
printf("图创建成功！\n");
}
/*
*G：不为空的图
*v：需要访问的顶点
*/
void VisitFun(MGraph G,int v){
printf("%c ",G.vexs[v]);
}
/*
*G：不为空的图
*v：其实访问的顶点
*/
void DFS(MGraph G,int *visited,int v){
visited[v] = 1; //将访问的结点设置为1
//访问这个这个顶点
VisitFun(G,v);
//寻找与这个顶点相邻的其他结点
for(int k=0;k<G.vexnum;k++){
if(G.AdjMatrix[v][k]==1){ //有边
if(visited[k]==0){ //且该顶点没有被访问过
//那么久递归调用DFS去遍历与这个边邻接的顶点
DFS(G,visited,k);
}
}
}
}
main() {
int visited[MAX_VERTEX_NUM];
//初始化访问标记数组 顶点访问则设置为1
for(int i=0;i<MAX_VERTEX_NUM;i++){
visited[i] = 0;
}
MGraph G;
CreateGraph(G);
DFS(G,visited,0);
}
正文到此结束
- 本文标签： c语言 算法
- 本文链接： https://www.it1997.com/article/49
- 版权声明： 本文由小陈没烦恼原创发布，转载请遵循《署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0)》许可协议授权
相关文章
热门推荐
近期评论
-
来自： 阅读更多 展开全文的功能是如何实现的
-
来自： 阅读更多 展开全文的功能是如何实现的
-
来自： 好用的截图工具FastStone Capture 带激活码）
-
来自： 留言板
-
来自： 留言板
